Феррари метод конечных элементов

Обновлено: 05.07.2024

Применение метода конечных элементов для расчёта электромагнита тормоза инвалидной коляски Текст научной статьи по специальности «Физика»

Аннотация научной статьи по физике, автор научной работы — Помогаев Г. В., Согрин А. И., Лютов М. А.

Рассмотрены вопросы применения метода конечных элементов при решении осесимметричных задач теории поля на примере электромагнитного тормоза для инвалидной коляски.

Похожие темы научных работ по физике , автор научной работы — Помогаев Г. В., Согрин А. И., Лютов М. А.

Текст научной работы на тему «Применение метода конечных элементов для расчёта электромагнита тормоза инвалидной коляски»

ПРИМЕНЕНИЕ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ ДЛЯ РАСЧЕТА ЭЛЕКТРОМАГНИТА ТОРМОЗА ИНВАЛИДНОЙ КОЛЯСКИ

Г.В. Помогаее, А.И. Согрин, М.А. Лютое г. Челябинск, ЮУрГУ

Рассмотрены вопросы применения метода конечных элементов при решении осесимметричных задач теории поля на примере электромагнитного тормоза для инвалидной коляски.

Во многих технических устройствах очень широко применяются электромагниты для выполнения функций, основанных на притяжении подвижной системы (якоря) электромагнитом. В связи с этим, встают вопросы более точного расчета данных устройств и в особенности его тяговой характеристики.

Как известно, сила тяги электромагнита равна частной производной энергии по перемещению:

где (У,„ - энергия магнитного поля, исследуемой системы;

х - координата перемещения.

Сила Р направлена таким образом, чтобы якорь стремился приблизиться к электромагниту. При этом энергия, запасенная в магнитном поле воздушного зазора, переходит в механическую работу, затрачиваемую на перемещение якоря.

В данной работе рассматривается вопрос расчета силы тяга электромагнита, изображенного на рис. 1.

4 вывод обмотки

Рис. 1. Общий вид электромагнита

Расчет произведен двумя способами. Первый основан на классическом подходе, рассмотренном в [1].

В данном случае изменение энергии магнитного поля рассматривается только в воздушном зазоре, не учитывается изменение энергии всей магнитной системы и поле рассеяния между якорем и магнитопроводом является плоскопараллельным. Данные допущения, по мнению авторов, является недостаточно точными, так как при перемещении якоря электромагнита имеются участки магнитной системы с насыщением и распределение магнитного шля имеет более сложный характер, что заметно может сказаться при расчете усилия.

По этому, предлагается расчет исследуемого электромагнита (см. рис. 1) на основе метода конечных элементов (МКЭ). Как известно, исследуемая область в МКЭ разбивается на конечные элементы различной конфигурации. В данном случае дискретизация пространства произведена с использованием треугольных элементов второго порядка, что повышает точность решения задачи. Условия симметрии позволяют ограничиться рассмотрением половины исследуемой области электромагнита.

Интерполяционный полином для квадратичного треугольного элемента осесимметричной задачи имеет вид:

где г - расстояние от оси симметрии до узлового потенциала;

г - ось симметрии.

При расчете осесимметричной задачи необходимо решить уравнение Пуассона в виде:

где А - векторный магнитный потенциал; вектор плотности тока;

/л - магнитная проницаемость среды.

При введении другой переменно Т = г ■ А данное уравнение принимает симметричный вид относительно производных по координатам г и г [2]:

где у ----магнитная проводимость среды.

Составляющие магнитных индукций по осям примут вид:

1 (Р¥ п 1еР¥ Вг=——,Вг=——. (4)

С учетом выше изложенного решение уравнения (3) связано с минимизацией функционала:

Вестник ЮУрГУ, № 9, 2005

Помогаев Г.В., Согрин А.И., Лютое М.А.

Применение метода конечных элементов для расчета ________электромагнита тормоза инвалидной коляски

Система уравнений, для решения задачи, получается из условия стационарности функционала

Коэффициенты матриц, получаемых при расчете производных, входящих в уравнение (5),

здесь к,-, щ - базисные функции, являющиеся полиномами переменных гиге коэффициентами а(.

Далее формируется глобальная матрица и вектор столбец правых частей. После этого, любым из известных способов производят решение системы линейных уравнений для каждой итерации до сходимости итерационного процесса.

Решение осесимметричной задачи для электромагнита, изображенного на рис. 1 представлено на рис. 2 при фиксированном воздушном зазоре.

Рис. 2. Распределение магнитного поля

МКЭ позволяет достаточно полно исследовать данный объект при различных изменениях как магнитной системы, так и электрических параметров.

На рис. 3 представлена зависимость тяговой характеристики исследуемого электромагнита от величины воздушного зазора ^ = /(<?).

Рис. 3. Тяговые характеристики электромагнита: 1 - механическая характеристика электромагнита, рассчитанная методом конечных элементов; 2 - механическая характеристика электромагнита, рассчитанная аналитически

На рис. 4 представлена зависимость тягового усилия исследуемого электромагнита от магнитодвижущей силы (МДС) Р-/(-?’) при фиксированном воздушном зазоре.

Рис. 4. Зависимость тягового усилия от МДС обмотки

1. Гордон А.В., Сливинская А.Г. Электромагниты постоянного тока. - М.: Государственное энергетическое изд-во, 1960. -447 с.

2. Демирчан КС., Чечурин В.Л. Машинные расчеты электромагнитных полей. -М.: Высшая школа, 1986. - 240 с.

3. Сильвестер П., Феррари Р. Метод конечных элементов для радиоинженеров и инженеров-электриков. - М.: Мир, 1986. - 229 с.

4. Сегерлинд Л. Применение метода конечных элементов. — М.: Мир, 1976. - 392 с.

Помогаев Г. В., старший преподаватель ЮУрГУ.

Согрин А.И., старший преподаватель ЮУрГУ.

Лютов М.А., начальник бюро расчетов отдела № 57, ОАО «НПО «Электромашина», г. Челябинск.

Научный форум dxdy

Ищу специалиста по методу конечных элементов!

В МКЭ ничего сложного нет. Главное литературу грамотную найти и пару библиотек для пре- и постпроцессинга.
На мой взгляд, самая интересная книга на русском - Сильвестер и Феррари "МКЭ для радиоинженеров и инженеров-электриков" (но она по расчету электромагнитных полей, я просто ими и занимался) и, конечно, Зинкевич.

Самая новая и достаточно полная - Это Зинкевич 5-е издание, на английском (Zienkiewicz O.C., Taylor R.L. Vol. 1. The finite element method. The basis). Там есть практически все , начиная от элементов и заканчивая восстановлением градиентов решения. Книга есть на этом сайте (http://lib.mexmat.ru/books/668).

Генераторы сеток - Handbook of Grig Generation , есть в инете в электронном виде, весит 107MB. Есть неплохие подборки статей и ссылок на литературу по генерации сеток (http://www-users.informatik.rwth-aachen.de/

Хранение матриц и решатели СЛАУ - есть разнообразные библиотеки, я бы посоветовал MTL и ITL. На мой взгляд, для решения СЛАУ наиболее применим метод сопряженных градиентов (CG) с предобуславливанием неполным разложением Холесского (Incomplete Cholessky Preconditioned Conjaguate Gradient, ICPCG), который используется в комерческих программах.

Для ускорения процесса решения СЛАУ и распараллеливания можно применить метод геометрической декомпозиции (Domain Decomposition). Тут только самая проблема как грамотно разбить матрицу на оптимальное количество частей. Наиболее шустрые алгоритмы разбинения - многоуровневые (Multilevel), есть хороший сайт одного из авторов алгоритмов - Karypis'a - с подборкой его статей, там же есть в свободном доступе его набор программ для разбинения METIS с исходными кодами.

Построение графиков - здесь лучше заглянуть на CodeProject, там есть есть хорошая подборка графопостроителей 2D-3D, на основе чего можно и свое написать.

Задание геометрии - также есть библиотеки, один Open CASCADE чего стоит. Но самое простое, на мой взгляд, это просто написать (или найти готовые) библиотеки чтения DXF-файлов (есть описание форматов файлов на сайте Autodesk) или фалов CATIA, и доделать их для себя.

Зинкевич 5-е издание.
Ух-ты! Спасибо за книжку. Стоит она конкретно.

Феррари метод конечных элементов

Методы конечных разностей и конечных элементов в задачах электромагнитной совместимости

Валетов Еремей Владимирович,

докторант Университета штата Мичиган, США.

Цель данной статьи – рассмотрение основных численных методов и их применения в задачах электромагнитной совместимости. Исторически сложилось так, что аналитические методы считались абсолютно истинным выражением процессов, происходящих в физическом мире. Однако обладая физической наглядностью аналитические методы имели значительный недостаток: они были предназначены только для анализов процессов с высокой степенью идеальности, что, к сожалению, в реальных исследовательских задачах недопустимо.

Аналитические методы и методы физико–математического моделирования

Для того, чтобы потом продолжить смотреть текущее видео, просто сохраните ссылку

С некоторой натяжкой к данным методам можно отнести и методы физико–математического моделирования. Данные методы начали интенсивно развиваться с 50 – 60-х годов ХХ века. Ввиду отсутствия или очень слабых возможностей вычислительной техники в то время преимущественно разрабатывались методы физического и аналогового моделирования. При физическом моделировании соответствующие величины оригинала и модели имеют одинаковую физическую природу. Аналоговые методы базируются на аналогии уравнений, описывающих процессы в оригинале и модели. При этом соответствующие величины, характеризующие оригинал и модель (величины - аналоги), имеют различную физическую природу.

Во многих случаях аналоговые методы имеют преимущества: наглядность получаемых решений, большая универсальность по сравнению с аналитическими методами, возможность моделировать процессы в реальном масштабе времени. К недостаткам аналоговых методов можно отнести следующие: трудоемкость изготовления аналоговых моделей; для обеспечения условий подобия требуются предварительные расчеты, которые плохо поддаются автоматизации и требуют повышенного внимания от исследователя. Указанных недостатков лишены численные методы.

Численные методы

С развитием цифровой вычислительной техники все большее распространение стали получать численные методы моделирования электромагнитных полей, основанные на пространственной и пространственно-временной дискретизации. Преимущества численных методов заключаются в том, что они позволяют получить искомый результат с учетом реальных свойств материалов и геометрии всех входящих в расчетную область тел [12].

Численные методы нацелены на непосредственное решение уравнений поля с граничными условиями, обусловленными геометрией задачи и самой задачей. Хотя они требуют большего объема вычислений, чем аналитические методы или экспертные системы, численные методы являются крайне мощным инструментом анализа задач электромагнетизма. Не делая заранее никаких предположений о том, какие полевые взаимодействия наиболее значимы, численные методы осуществляют анализ всей геометрии исследуемой конфигурации полностью. При этом геометрия задачи задается в виде входных данных [1].

Как известно, все электромагнитные процессы в межсоединениях ПП описываются посредством уравнений Максвелла [8]. Из системы полных уравнений Максвелла путем несложных математических преобразований можно получить следующие уравнения:

Это уравнения Гельмгольца и они являются исходными при проведении анализа волновых процессов (в частности электромагнитного излучения) [4].

Для решения данных уравнений необходимо правильно выбрать и задать граничные условия. Однако, при моделировании электромагнитного излучения возникают трудности, связанные с постановкой условий в открытой области, где напряженность поля неизвестна. Моделирование электромагнитного поля на бесконечности, в том числе, связано с поиском таких методик постановки граничных условий, которые будут обеспечивать высокую точность решения уравнений поля, даже если граничные условия ставятся на достаточно близком расстоянии от исследуемого объекта.

Именно задачи подобного класса сдерживали применение метода конечных разностей в области электромагнитной совместимости.

Непосредственное применение численных методов к открытой (или, другими словами, бесконечной) области, вмещающей бесконечное число узлов, приводит к бесконечной системе алгебраических уравнений, решение которой не может храниться в конечной памяти вычислительной машины. Поэтому необходимо осуществлять редукцию этой системы, исходя из общих, достаточно универсальных соображений, например, искусственно ограничивая открытую область либо идеальной, либо поглощающей границей. Идеальную границу целесообразно использовать в тех случаях, когда заранее известно, что решение краевой задачи в открытой области достаточно быстро убывает на бесконечности. В частности, для уравнений Лапласа и Пуассона метод ограничения открытых областей идеальными границами был рассмотрен в [3].

При рассмотрении в открытых областях краевых задач для уравнения Гельмгольца быстрого убывания поля на бесконечности, как правило, не наблюдается. Поэтому оказывается, что вместо идеальных границ в этом случае необходимо использовать поглощающие границы. Детальный обзор подобных граничных условий был сделан в [ 1 ] .

Современный подход в постановке поглощающих граничных условий состоит в применении так называемого материального поглотителя. Данные граничные условия реализуются путем окружения расчетной области материалом с электромагнитными потерями, который ослабляет проходящее через него электромагнитное поле. Идея использования материальных поглощающих граничных условий была изложена достаточно давно. Однако первые поглощающие граничные условия не обеспечивали достаточно малого коэффициента отражения от границы, поскольку характеристический импеданс материальной границы был согласован с импедансом вакуума только при нормальном падении волны [9].

Использование материальных поглощающих условий получило новый толчок в 1994 году, когда был создан идеально согласованный слой (в латинском сокращении PML – Perfectly Matched Layer), изначально описанный в [10]. Метод разбиения компонент поля, изначально используемый для построения PML можно рассматривать как имеющий исключительно математический смысл и не имеющий никакого соответствия физическому миру. Однако в [11] он был получен с помощью продолжения функций, описывающих поле, в комплексную плоскость. Хотя идеально согласованный слой считается физически не реализуемым, в [13] была физически реализован слой, имеющий аналогичные характеристики. Надо заметить, что отечественные авторы отстают от зарубежных в части применения идеально согласованного слоя для задач моделирования электромагнитных полей. Среди отечественных авторов, следует выделить работы И.В.Белова [2] для моделирования распределения электромагнитных полей в помещениях.

Пример покрытия PML показывается на рис. 1.

Рис. 1. Построение идеально согласованных слоев PML, окружающих объект.

После установления слоя PML, далее необходимо задать границы на наружной поверхности. Самый простой путь состоит в том, чтобы ограничить поле или идеальными электрическими проводниками (PEC) или идеальными магнитными проводниками (PMC). Обычно использование PEC уменьшает размер задачи.

Существует несколько различных методов для решения задач, подобных анализу электромагнитного излучения (ЭМИ). В настоящее время при анализе ЭМИ используются следующие основные методы:

- метод конечных разностей во временной области;

- метод конечных элементов;

Несмотря на свое формальное отличие в названии, по сути, данные методы являются подобными.

Широкое использование и развитие численных методов началось с методов конечных разностей (МКР) (или методов сеток). Эти методы основаны на замене дифференциальных операторов в уравнениях математической физики конечно-разностными операторами в соответствии с построенной сеткой (пространственная дискретизация области и ее границ заключается в построении сетки, состоящей из узлов и ребер). Путем такой замены дифференциальные уравнения в частных производных преобразуются в систему алгебраических уравнений относительно узловых величин. Проблемы построения и свойства систем конечно-разностных уравнений рассмотрены в [6]. В случае однородной среды переход к разностным уравнениям осуществляется путем простого применения конечно-разностных операторов. Для уточнения аппроксимации частных производных в состав этих операторов могут включаться конечные разности высших порядков. В случае кусочно-неоднородной среды к узлам, принадлежащим поверхностям раздела сред, вместо обычных разностных операторов применяются условия сопряжения, отражающие скачкообразные изменения частных производных. Аппроксимация частных производных по обе стороны от границы раздела сред выражается также через конечные разности. Граничные условия Дирихле учитываются простым заданием искомых величин в граничных узлах. Граничные условия Неймана или Коши аппроксимируются с помощью конечно-разностных операторов. Главным недостатком МКР является трудность в анализе непрямолинейных границ (которые имеют место в пакетах программ специализированного применения) [8].

Основным свойством получаемых систем конечно-разностных уравнений является ленточная или профильная структура матрицы коэффициентов. Ширина ленты или профиля определяется нумерацией узлов, регулярностью сетки, максимальным порядком конечных разностей, используемых для аппроксимации частных производных. Как правило, матрица коэффициентов характеризуется слабой заполненностью внутри ленты или профиля даже при оптимальной нумерации узлов, поэтому для ее хранения в памяти ЭВМ часто применяется технология разреженных матриц. Методы решения систем сеточных уравнений определяются их свойствами. Методы матричной прогонки основаны на гауссовом исключении или факторизации применительно к ленточным матрицам. Другие прямые методы основаны на различных видах разложения на множители применительно к разреженным матрицам. Основным недостатком прямых методов является плохая приспособленность их к компактным схемам хранения разреженным матриц (при факторизации происходит их заполнение). Поэтому приходится использовать итерационные методы.

Помимо конечно-разностных методов решения задач математической физики существуют методы, обладающие свойствами как численных, так и аналитических: методы интегральных уравнений, вариационные и проекционные методы (методы взвешенных невязок и связанные с ними методы конечных (МКЭ) и граничных элементов).

Метод конечных элементов основан на интегральной формулировке граничной задачи [7]. Вместо дифференциальных уравнений с частными производными устанавливаются соответствующие функционалы. Исследуемая область в зависимости от размерности задачи делится на плоские или объемные элементы, в которых неизвестное распределение поля аппроксимируется полиномами. Использование метода Рэлея-Ритца позволяет затем получить систему линейных алгебраических уравнений. Поскольку некоторые из выделенных элементов включают границы исследуемой области, полученная система уравнений может быть решена для внутренних точек. Метод конечных элементов имеет некоторое преимущество перед методом конечных разностей в гибкости, так как с его помощью легко учитываются сложные границы. Порядок аппроксимирующих полиномов дает дополнительную свободу при численном расчете. Недостатком метода является большая требуемая память ЭВМ.

Метод моментов, наряду с методом конечных разностей во временной области, наиболее широко распространен в современных пакетах анализа ЭМИ. В основе метода моментов - решение интегрального уравнения. Данный метод преобразует интегральное уравнение в систему алгебраических уравнений, которая решается численным способом. Сам метод представляет собой развития метода Галеркина. В методе моментов используется базовая треугольная функция, и дельта-функция как тестовые (проверочные) функции. Если базовые и тестовые функции различны, как в методе моментов, то правая часть системы уравнений приобретает как бы «момент», вместо нулевой правой части, как в методе Галеркина [5]. Хотя с точки зрения решения этой системы эти подходы эквивалентны. В настоящее время этот метод наиболее широко применяется для моделирования ЭМИ иностранными авторами, однако следует отметить один весьма важный недостаток данного метода: матрица получается полностью заполненной, а не разреженной, как в МКЭ, вследствие чего значительно увеличивается время вычисления.

Приведем основные характеристики численных методов, используемых при прогнозировании ЭМИ от ЭС и их компонентов. Порядок следования методов будет соответствовать повышению аналитической сложности и, соответственно, уменьшению их гибкости. Результаты сравнения методов приведены в табл. 1.

Моделирование стержневых систем методом конечных элементов

В методе конечных элементов основной идеей является замена исходной непрерывной системы (деформированного тела) множеством связанных математических точек. Будем считать, что определена неподвижная система координат (глобальные координаты), по отношению к которой определяется движение мат. точек. В дальнейшем будем называть узлами мат. токи принадлежащие деформированному твердому телу, для которых указаны начальные координаты и нумерация, причем каждая точка имеет уникальный номер. Количество таких точек будем считать конечным.

Некоторое множество этих точек принимаем за вершины многогранника, причем множество всех возможных многогранников определенное на множестве узлов отличается тем, что многогранники не пересекаются между собой и полностью заполняют объем тела. Последнее требование может быть ослаблено в близи границ тела. В том смысле, что грань многогранника, вершины которой принадлежат поверхности может не принадлежать поверхности тела.

Такие многогранники, каждому из которых приписаны уникальные номера называются конечными элементами (КЭ). Если установлено однозначное соответствие между номерами многогранников и номерами узлов, которые являются их вершинами, то говорят, что определена сетка КЭ. Переход от непрерывного тела к его конечно-элементной модели осуществляется путем выбора способа определения некоторой искомой функции в произвольной точке объема по ее значению в узлах. Функция которая осуществляет эту интерполяцию называется функцией формы. Основное отличие метода КЭ от других численных методов заключается в том, что интерполяция осуществляется только по узлам принадлежащим КЭ.

Функции формы реализующие кусочную интерполяцию разделяют следующим образом:

1. Функции формы должны принадлежать множеству функций, интегрируемых в пределах КЭ.

2. Функции формы с определенным номера k должна принимать значение =1 в этом узле и =0 во всех других узлах.

3. Функция формы должна быть однозначной в пределах объема КЭ.

Если производится интерполяция в пределах некоторой функции, для которой не выполняется условие 2, но выполняется условие 1 и 3, то эту так называемую аппроксимирующую функцию следует нормировать составляя систему уравнений вида

Для определения значений функции в узлах в рамках МКЭ используются различные функционалы, минимум которых соответствует реальному значению исходной функции. Таким функционалом может быть невязка между строгим решением уравнения равновесия и приближенным решением; невязка между значением функции на границе и заданными краевыми условиями: Вариационный функционал Лагранжа (принцип возможных перемещений), вариационный функционал Костельяна (принцип минимума дополнительной работы) и т.д.

Выбор вариационного функционала определяет модификацию метода КЭ. Если используются функционалы невязки между значениями функции на границе или некоторыми дифференциальными операторами над ней в объеме, то МКЭ можно считать дискретным вариантом метода Бубнова - Галеркина. Если используется функционал Лагранжа, то МКЭ можно трактовать как вариант метода Ритца.

Метод конечных элементов

Метод конечных элементов – это метод приближенного численного решения физических задач. В его основе лежат две главные идеи: дискретизация исследуемого объекта на конечное множество элементов и кусочно-элементная аппроксимация исследуемых функций.

Применение метода конечных элементов

На практике применение метода FEM, также известного как FEA (анализ методом конечных элементов), началось в начале 1960-х годов в авиационной и аэрокосмической отраслях, но очень скоро метод нашел применение в автомобилестроении. Сегодня метод исполь­зуется во всех областях деятельности, включая прогнозирование погоды, медицину, и многие приложения автомобилестроения, от расчета компонентов двигателя и шасси до прогнози­рования поведения кузова при столкновении.

Имеются два различных способа при­менения FEM. Изначально использовался «черный ящик» FEM, который входил в со­став всех программ CAD (компьютеризован­ного проектирования) и предназначался для грубых расчетов, выполняемых инженером- конструктором (например, при конструиро­вании бампера), но затем применение метода было оставлено за специалистами по при­кладным программам FEM (например, пред­назначенным для расчета кузова, разработки мостов или расчета динамики движения).

Программное обеспечение FEM

В программное обеспечение FEM входят препро­цессор, постпроцессор и собственно программы FEM. Создание сети, т.е. разбиение на элементы, в основном, выполняется в препроцессоре на основе геометрии CAD, которая считывается непосредственно или через нейтральные ин­терфейсы, такие как IGES (исходный стандарт обмена графическими данными), VDA-FS (интер­фейс для технических характеристик элементов и точек, установленных союзом немецких автомобилестроителей) или STEP (стандарт по обмену данными моделей изделий). Программа FEM рас­считывает сформулированную таким образом модель вычислений. Полученный результат за­тем отображается в графической форме в пост­процессоре (например, распределение нагрузок в виде линий одного цвета, показ механических напряжений в форме анимации).

Основные сведения по применению метода конечных элементов

Подобно всем числовым методам, FEM пред­ставляет собой процесс аппроксимации. В механике, основной сфере применения FEM, ограничения, налагаемые на этот метод, описываются следующим образом.

Малые перемещения за один шаг решения

Тела движутся по траекториям, которые обычно являются кривыми высшего порядка. В соответ­ствии с основным принципом линеаризации, эти перемещения ограничиваются прямолинейными траекториями, которые могут быть описаны ли­нейными уравнениями. Будучи перенесенными к экстремальным точкам элементов (узлам), они также перемещаются по прямой линии. Таким образом, узлы способны правильно совершать только очень малые перемещения (узел повора­чивается менее чем на 3,5°). Фактическое движе­ние вдоль любой траектории или нелинейное по­ведение материала описывается, таким образом, линейными перемещениями, шаг за шагом, при большом количестве малых шагов.

Точность вычислений

Система линейных уравнений составляется и решается при ограниченной точности вы­числений, производимых компьютером. Обычно для сохраненного в памяти числа используются 8 байтов (= 64 бита) с точно­стью вычислений до 13 значащих цифр, т.е. только первые 13 цифр числа могут быть представлены точно. Четырнадцатая цифра и все последующие цифры в этом числе яв­ляются случайными числами. Таким образом, это исключает возможность каких-либо раз­личий по жесткости отдельных компонентов модели. Например, при расчете деформаций каркаса кузова необходимо при измерениях деформации кузова, заменить пружины мо­ста жесткими опорами.

Интерпретация результатов

Большая опасность заключается в том факте, что формальная модель вычислений, пра­вильно сформулированная в начале, может создать действительно выразительные цвет­ные изображения, однако демонстрируемые результаты могут концентрироваться вокруг факторов, заслоняющих реальность.

Проблемы, возникающие в результате вы­шеуказанных ограничений, должны, следова­тельно, быть идентифицированы и помечены программой вычислений, с тем чтобы менее опытный пользователь также мог легко по­лучать правильные результаты.

Области применения FEM

Физика, с точки зрения приложений в тех­нике, в общем случае подразделяется на пять разделов: механика со статикой и кинемати­кой (например, кузов, мосты); динамика и акустика (например, шум, создаваемый авто­мобилем); термодинамика (например, темпе­ратурный режим в двигателе); электричество и магнетизм (например, катушка зажигания и датчики); оптика (например, фары). Что касается метода FEM, всегда проводится раз­личие между:

• Линейными и нелинейными, статическими и динамическими проблемами с деформа­циями, как неизвестными величинами для вычисления механических напряжений и динамического анализа;
• Стационарными (вневременными) и не­стационарными (зависящими от времени) потенциальными проблемами (например, температура, звуковое давление, электри­ческий или магнитный потенциал) с потен­циалами в качестве неизвестных величин;
• Связями различных областей, например, для расчета температурного поля и ре­зультирующих деформаций, напряжений и усилий в линейной статике вовремя пу­ска двигателя.

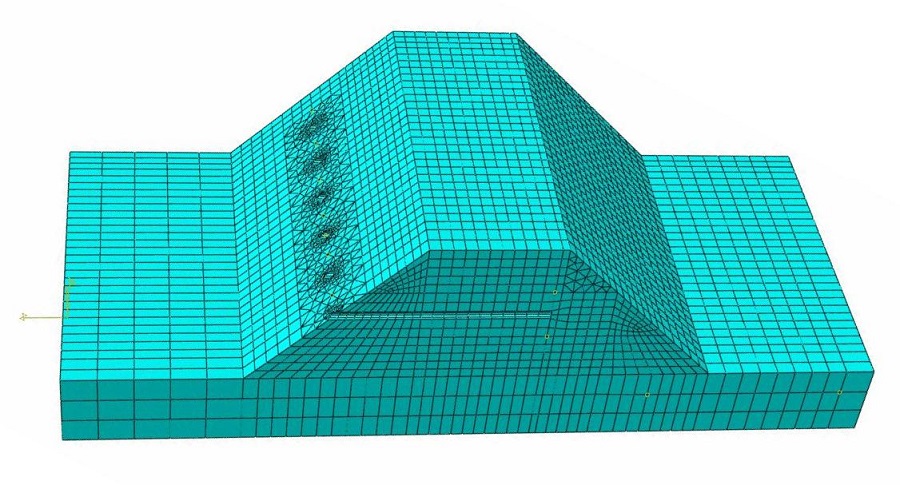
Элементы FEM

Свойства элементов определяют наиболее важные рабочие характеристики программы FEM. Качество элемента выражается степе­нью выбранной функции математического описания. Проводится различие между эле­ментами с линейным и квадратным описа­нием, которые распознаются по срединным узлам (находящимся в серединах сторон). Таким образом, качество модели вычислений зависит не только от крупности используе­мой сетки, но также в значительной степени от функции описания.

Линейные элементы

Оболочковые элементы

Объемные (сплошные) элементы

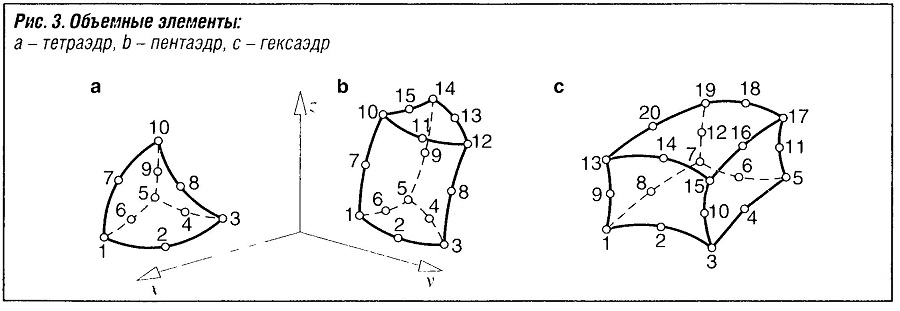
Моделирование и оценка результатов

Наиболее важной функцией при использова­нии программы FEM является задача создания исходных данных в качестве модели вычисле­ний с использованием препроцессора. На эту задачу обычно уходит много времени. Поль­зователь должен стремиться достигнуть этой цели как можно меньшим количеством эле­ментов и узлов (однако, следует иметь в виду, что модель расчета, например, кузова может иметь примерно от трех до четырех миллионов узлов). Для этого пользователю следует обла­дать определенным опытом, а также он должен точно знать параметры используемых элемен­тов (см. ниже примеры FEM). Они могут не­сколько различаться в каждой программе FEM.

Все результаты FEM доступны в форме перечня или в формате данных постпроцес­сора и, следовательно, могут быть показаны в виде графика (см. примеры FEM). В этом смысле постпроцессор предлагает все воз­можные формы отображения результатов.

Примеры FEM

В качестве примера приведем моделирова­ние, выполненное на основе геометрии CAD с использованием программы FEM ТР2000. Исходные данные для модели вместе с пред­ставлением результатов в цвете можно также найти на странице интернета.

В действительности все тела являются трех­мерными. При моделировании, для экономии времени и средств, часто выбирается упро­щенное решение. Например, намного легче вы­полнить автоматическое сеточное разбиение плоской поверхности в оболочковых элемен­тах, чем представлять тело в виде его объем­ных элементов. Часто используемая сетка те­траэдров, которую в настоящее время создает каждый препроцессор для любой объемной геометрии, не всегда оправдывает ожидания.

В автомобилестроении структурные ком­поненты являются либо толстостенными и сплошными (например, двигатель, транс­миссия, мосты, колеса) и моделируются при помощи объемных элементов, либо они из­готавливаются из тонкого листового металла (например, кузов автомобиля или кабина гру­зовика) и моделируются с использованием оболочковых и линейных элементов.

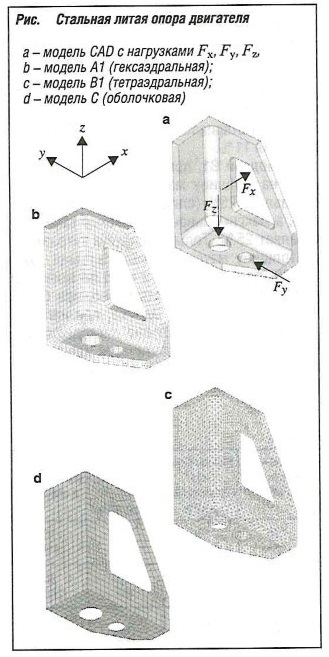
Пример 1: литая стальная опора двигателя как модель на основе оболочковых и объемных элементов (линейная статика)

Приняты следующие свойства материала:

Для моделей А и В свойства элементов опреде­ляются типом элемента «сплошной» (объемный) с тремя степенями свободы узлов v_x, v_y и v_z. Для модели С свойства определяются типом элемента «пластина» (оболочковый элемент) с шестью степенями свободы узлов v_x, v_y, v_z, d_x, d_y, d_z и постоянной толщиной d= 3,75 мм.

Условия опор

Нагрузки

Примечание: применение «изолирован­ных» отдельных нагрузок допускается только при использовании линейных элементов.

Результат

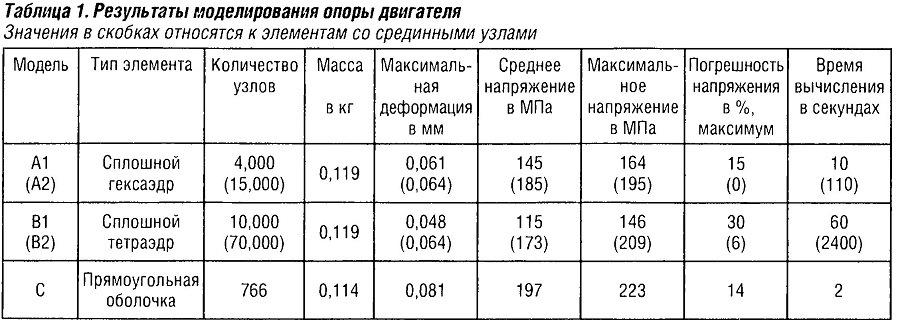
Объемные элементы очень чувствительны к неправильно апроксимированным распре­делениям нагрузок. Следовательно, объем­ные элементы должны всегда испытывать только поверхностные нагрузки.

Пример 2: трубчатый каркас кузова

Целью является выполнение анализа ме­тодом конечных элементов кузова в виде объемного каркаса без листовой обшивки, включая оптимизацию веса и жесткости, на примере мини-пикапа (не реальный автомо­биль).

Коробчатый/трубчатый профиль:

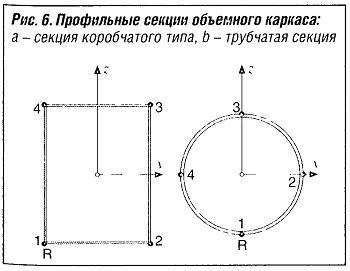
• Площадь поперечного сечения: А = 621/427;
• Уменьшенные поперечные сечения (в об­ласти сдвига): A_redl = 325/227; A_redll = 219/227;
• Главные моменты инерции: I_I = 1 348 306/247 168; I_II = 869 596/247 168;
• Момент инерции при кручении: I_t = 1 606 083/494 261;
• Крутящий момент сопротивления сечения: W_t = 7334/2177;
• Расположение главных осей инерции по отношению к дороге: a = 0°;
• Максимум четыре точки концентрации напряжений:

• L₁= 4 114 (максимум);
• L₂ = 2 650;
• W₁ = 1 517 (максимум);
• W₂ = 1 147 (спереди);
• W₃ = 1 374 (сзади);
• Н₁ = 1 402 (макс.);
• Н₂ =1 315;
• H_з = 469 (коробчатый профиль).

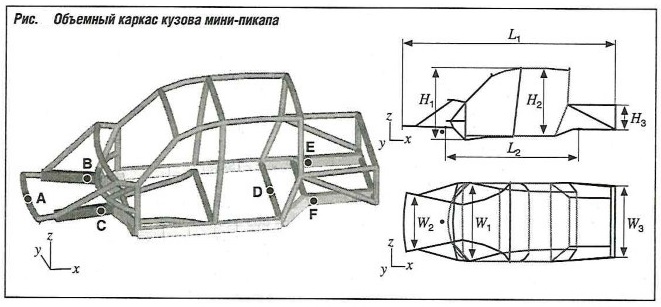
Конструкция

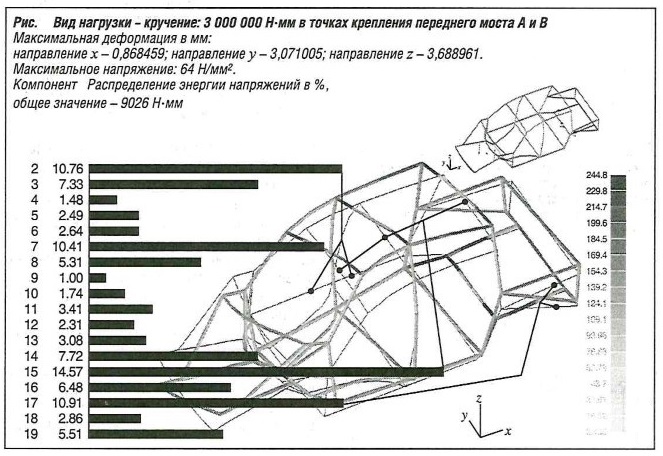
Условия опор:

Степени свободы/динамика в свободном со­стоянии: без опор, кузов свободно вибрирует на пру­жинах.

Напряжения

опоры переднего моста С: F = 3 593,7 Н .

Степени свободы/динамика в свободном со­стоянии: только массы, на которые действует сила тя­жести 170 кг, без дополнительных масс.

Результаты

Степени свободы/динамика в свободном со­стоянии:

Линейная статика:

• Деформации х, у, z во всех узлах;
• Силы и моменты реакции, действующие на все элементы, энергия напряжений, при­ходящаяся на элемент и компонент в %.

Оптимизация веса и жесткости

Формула вычислений для оптимизации веса и жесткости известна, начиная с 1960-х годов (максимальная погрешность для двойной жесткости -10 %). Изменение жесткости всей конструкции (в %) получено посредством умножения изменения жесткости компонента на долю энергии напряжений для компонента и деления результата на 100.

Эта формула используется специально в целях оптимизации практически во всех критичных для автомобиля случаях нагрузки при кручении с учетом других видов нагрузки. Таким образом, конструкция может быть усилена при помощи стоек, воспринимающих основную часть нагрузки, а вес может быть снижен за счет стоек, воспринимающих меньшую часть нагрузки.

Применение формулы

Второй компонент (см. рис. 8): компонент 6 (линейный усилитель­ный элемент, G = 11,14 кг с долей энер­гии напряжений 2,64%) дает изменение (2,64 х 250)/100 = 6,6 % (т.е. очень неболь­шое снижение момента кручения между мостами, когда жесткость (момент инерции) этого компонента уменьшается в 3,5 раза (на 250%). В этом случае при уменьшении диа­метра трубы с 70 до 50 мм снижение массы составляет 3,34 кг.

Результат

Диаграммы распределения энергии напря­жений для других случаев нагрузки (здесь не показаны) показывают, что это также относится к крутильным колебаниям и не имеет значения для изгиба. Таким образом, можно значительно повысить для этого ку­зова жесткость при кручении и жесткость на изгиб и безопасно снизить общую массу посредством уменьшения поперечных се­чений компонентов, имеющих избыточные размеры.

Феррари метод конечных элементов

Каковы концептуальные различия между методом конечных элементов (МКЭ) и методом конечных разностей (МКР)? Возможно, вы уже задавались этим вопросом, если использовали в своей работе метод конечных элементов и осознали, что ваши отношения достаточно серьёзны, чтобы углубиться в теорию, лежащую в его основе. Хочу вас обрадовать – вы попали по адресу!

Мой блог как раз и посвящён конечноэлементному анализу от базового до углублённого уровня, и в этой статье я планирую «углубиться»… если вас это не пугает – добро пожаловать!

Начнём с того, что метод конечных элементов (по-английски FEM – Finite Element Method) и основанный на нём конечноэлементный анализ (FEA – Finite Element Analysis) – это один из способов численного решения дифференциальных уравнений, описывающих физические явления.

Да-да, любую тему я предпочитаю начинать с самых основ, детально разбирая каждое понятие, ведь только так можно добиться истинного понимания.

Если вы уже знакомы с уравнениями, описывающими физические поля, и основами численных методов, то в различиях между методом конечных элементов и методом конечных разностей вы разберётесь быстро… Можете сразу начать с выводов, а потом просмотреть статью, если что-то будет не ясно.

Если же фундаментальных знаний вам пока не хватает, я постараюсь помочь восполнить пробелы. Помните, всегда важно добраться до сути понятий, а не ограничиваться одним лишь определением (в противном случае, учебники можно было бы заменить на словари).

Физические уравнения – как мы к ним пришли?

На протяжении многих веков человечество стремилось изучить природу окружающего нас мира. Ведь для того, чтобы иметь возможность контролировать, изменять и улучшать условия нашей жизни, необходимо вначале разобраться, как всё устроено. Постепенно учёные создали модели, описывающие окружающую нас действительность на языке уравнений, что позволило значительно продвинуться в изучении различных природных явлений.

Ещё с древних времён люди умели добывать огонь (этот момент в истории даже нарекли началом цивилизации), но лишь несколько столетий назад людям удалось понять, как именно тепло от этого огня распространяется в различных средах. Кстати, если вас интересует явление теплопередачи, советую ознакомиться с моей статьёй по этой теме.

Но как именно учёным удалось понять процессы теплообмена? Они выполнили ряд экспериментов и на основе полученных данных вывели некоторые уравнения. Эти уравнения позволили сформулировать законы. Затем, рассматривая совместно несколько законов, учёные построили теории и вывели ещё более мощные уравнения, которые позволяют раскрыть ещё больше загадок природы.

Но чем более сложными и обобщёнными становились уравнения, тем труднее было находить для них точные аналитические решения. Возникла необходимость изобрести что-то новое. инструмент, который дал бы возможность каждому физику решать эти уравнения, не тратя годы на попытки получить аналитическое решение, которого для конкретной задачи может даже и не быть. Именно с этой целью и были изобретены численные методы.

Как численные методы помогают решать физические уравнения?

Хотим мы того или нет, физические процессы обычно приходится описывать сложными дифференциальными уравнениями или даже системами таких уравнений. Если вы не сталкивались с решением дифференциальных уравнений, то у вас может возникнуть ошибочное мнение, что в них нет ничего особенного. «Почему нельзя просто найти решение, получить искомую функцию и вычислить результат?» – спросите вы.

Что ж… дифференциальные уравнения «немного» сложнее, чем вам кажется.

Сложность уравнений сильно возрастает, как только нам требуется учесть зависимость от времени. Не знаю, почему именно время является самым проблемным параметром, но если у вас на этот счёт есть какие-то идеи, поделитесь ими, пожалуйста, в комментариях к исходной статье. Обычно дифференциальные уравнения для описания физических процессов включают в себя зависимости не только от времени, но и от трёх координат в пространстве, а зачастую и от других переменных (например, от плотности жидкости при решении задач гидрогазодинамики).

Чтобы получить решение таких сложных задач, применяются следующие основные подходы:

• максимальное упрощение исходной модели физического процесса – например, можно исключить зависимость от времени, если для рассматриваемой задачи допустимо принять, что она является статической (стационарной);
• разделение модели на более мелкие и простые модели;
• применение приближённых численных алгоритмов, чтобы максимально точно аппроксимировать истинное решение.

Метод конечных элементов как раз и является одним из численных методов.

Является ли МКЭ единственным методом решения физических уравнений?

1. Метод конечных элементов (МКЭ).
2. Метод конечных объёмов (МКО).
3. Метод конечных разностей (МКР).
4. Метод граничных элементов (МГЭ).

В этой статье рассмотрены МКЭ и МКР, и я хочу вначале привести их краткое описание по отдельности, а потом поговорить о сходствах и отличиях.

Что представляет собой МКЭ?

Одной из ключевых характеристик метода конечных элементов является использование дискретизации для преобразования непрерывной области в набор (сетку) элементов типовой формы. Численные алгоритмы часто основаны на представлении исходной задачи в виде большого числа небольших повторяющихся задач – в таком виде компьютер сможет выполнить расчёт наиболее эффективно.

В теоретических моделях мы часто рассматриваем так называемые «бесконечно малые объёмы», которые стремятся к точке. Кстати, о бесконечно малых и конечно малых объёмах я рассуждал в своей статье о напряжениях (на английском языке), советую ознакомиться. Так вот, к сожалению, при выполнении расчёта численными методами невозможно аппроксимировать уравнения в бесконечно малых объёмах, потому что количество таких объёмов будет бесконечно большим, а с такой задачей не справится ни один компьютер. Также не получится задать одну непрерывную расчётную область сложной формы. Поэтому нам необходимо разбить расчётную область на отдельные элементы конечного размера. Кстати, под расчётной областью я понимаю геометрический объём (в трёхмерной постановке) или фигуру (для двумерных задач), в рамках которых рассчитывается физический процесс.

Для построения сетки конечных элементов компьютеру необходимо задать начало и конец. Необходимо как-то задать место, с которого алгоритм начнёт рассматривать расчётную область, затем задать, какой фрагмент он должен рассмотреть следующим, и так далее, пока не будет рассмотрена вся область.

После того, как расчётная область будет разбита на сетку конечных элементов, мы сможем записать уравнения для каждого из этих элементов, собрать все эти уравнения вместе с использованием принципа суперпозиции и, наконец, получить решение для всей расчётной области. Конечно, в таком описании я упустил многие важные этапы и понятия, оставив только то, что является основным для понимания различия между МКЭ и МКР.

А что же представляет собой МКР?

Метод конечных разностей, как и МКЭ, является одним из численных методов для решения физических уравнений. МКР тоже использует дискретизацию, но она производится другим образом, из чего вытекают отличия в подходах к составлению и решению уравнений. Вместо конечных элементов решение находится только в отдельных точках расчётной области.

Давайте в качестве примера рассмотрим задачу теплопроводности в стержне. Как и для любого численного метода, для метода конечных разностей понадобятся описывающие задачу дифференциальные уравнения, граничные условия и характеристики расчётной области.

В данном случае мы заменяем непрерывный стержень всего тремя узлами, в которых будем искать значения исследуемых физических полей. Исходное дифференциальное уравнение в общем виде выглядит так:

При использовании МКР мы заменяем все производные отношением конечных разностей (с использованием теоремы Тейлора):

Теперь нам остаётся только записать граничные условия, собрать всё вместе, и мы можем получить ответ для температуры в узлах стержня, решая при этом обычные алгебраические уравнения вместо дифференциальных. В этом и заключается суть метода конечных разностей.

Так МКЭ или МКР?

Что ж, теперь, когда я описал оба метода, вы, вероятно, догадываетесь, к чему я всё это вёл. Как МКЭ, так и МКР являются численными методами решения дифференциальных уравнений, описывающих физические явления. И тот, и другой метод способны обеспечить получение результата с достаточной с практической точки зрения точностью, поэтому сфера их применения обусловлена скорее особенностями и удобством реализации для конкретного класса задач.

В МКР расчётная область дискретизируется в виде сетки узлов, и результаты определяются только в этих узлах, в то время как в МКЭ результаты определены в каждой точке расчётной области и находятся с помощью функций формы, вычисляемых для конечных элементов. В связи с этим МКР обычно требует меньшей вычислительной мощности для решения уравнений и обеспечивает высокую скорость расчёта, но это приводит к менее «точным» результатам (только в узлах).

Для многих задач, например, при решении задач вычислительной гидрогазодинамики, критичным недостатком МКР является несоблюдение законов сохранения массовых и тепловых потоков. Это происходит из-за того, что МКР достаточно грубо аппроксимирует дифференциальные уравнения (только в узлах), а в МКЭ предусмотрено интегрирование по объёму конечного элемента. Эта особенность сильно ограничивает применение МКР, даже несмотря на высокую скорость расчёта.

В практических задачах чаще всего используется МКЭ. Для этого метода накоплен многолетний опыт успешного применения в различных инженерных отраслях и для различных дисциплин (таких как, механика, акустика, гидрогазодинамика, термодинамика, гидравлика и т.д.). МКЭ, безусловно, более популярен, чем МКР, и реализован в различных вариантах во многих программных продуктах.

Различие между МКЭ и МКР – подводим итоги

• МКР – это более старый метод, чем МКЭ, он требует меньшей вычислительной мощности, однако не применим для многих задач из-за погрешностей дискретизации.
• МКЭ позволяет получить более точные результаты (особенно на элементах второго порядка), но требует большей вычислительной мощности, а также он более требователен к качеству расчётной сетки.

—————————————————————————————————————-
Я очень хочу помочь инженерам (и студентам), которые только начинают решать задачи методом конечных элементов, лучше и быстрее разобраться в его основах.

Если вам понравилась эта статья, вот как вы мне можете помочь:

1- Поделитесь этой статьёй на Linkedin, facebook, twitter или на своём форуме, чтобы ещё больше людей разобрались в основах численных методов.
2- Напишите в комментариях к исходной статье, что вы узнали из неё, что ещё хотели бы узнать, и какие вопросы у вас остались. Это даст мне идеи для написания новых статей.
3- Подпишитесь на e-mail рассылку, чтобы первыми получать мои новые статьи (и не только)!

Благодарю за внимание!

Cyprien Rusu, ваш проводник по численным методам ;-)

Средняя температура по одной или нескольким граням тел в ANSYS Mechanical (Worbench)

В модуле ANSYS Mechanical (Workbench) есть инструмент, который позволяет получить максимальную или минимальную температуру

Читайте также:

  
• Схема выхлопной системы сузуки джимни
  
• Замена коробов на ниве своими руками
  
• На чери тигго т11 загорелся
  
• Фальшпол мазда 3 bk
  
• Дэу нексия рхх обучение